眾所周知，目前的大模型大多基於 Transformer 架構。Transformer 的核心結構是多頭自注意力模型（multi-head self-attention model）。
大模型的一個重要能力是所謂的「上下文學習」。具體來說，當大模型的參數訓練好之後，用戶和大模型的交互方式，是通過提供上文來獲得大模型的下文，這時大模型的參數是固定的。
當所提供的上文包含一些關於同一主題的輸入輸出例子時，大模型可以根據給的這些例子，學到這些例子背後的主題，從而可以在給到一個新輸入時，回答正確的輸出。
比如，上文可以是：
（來源：資料圖）
這時，Claude 3 大模型的回答是：
（來源：資料圖）
由圖可知，Claude 根據這些例子意識到「+」其實代表著減法，故能針對「10+5=？」這一新問題給出正確回答。
上下文學習，是大模型的一個基礎能力。使用大模型時的其他更複雜方式比如 Chain-of-thought reasoning，都是以此為基礎。
但是，從原理來看上下文學習的機制並不是很清楚。很大原因在於大模型作為一個系統，它不僅非常複雜，而且模型參數非常多，訓練數據也非常大。
為了更好地理解上下文學習，美國史丹福大學團隊曾在 GPT-2 架構之下，針對大模型如何使用上下文，學習解決簡單的回歸預測進行了研究。
其發現當使用簡單函數的數據來訓練大模型時，訓練好的大模型，可以通過上下文學到這些簡單函數。
一個特別的例子便是線性函數。這時的訓練數據是一些線性數據 x_1，w x_1，…，x_n，w x_n，其中 w 是高斯隨機向量。
換句話說，每個「句子」里都有 n 個線性函數的例子，而這個線性函數是隨機的。
（來源：https://arxiv.org/pdf/2208.01066.pdf）
以此為啟發，美國耶魯大學助理教授楊卓然和團隊，希望可以從理論上研究這種訓練過程是否收斂、以及收斂到哪裡，也希望釐清多頭自注意力結構到底是如何實現上下文學習的。
隨後，他和所在團隊考慮了一個最簡單的模型：一層多頭自注意力模型。
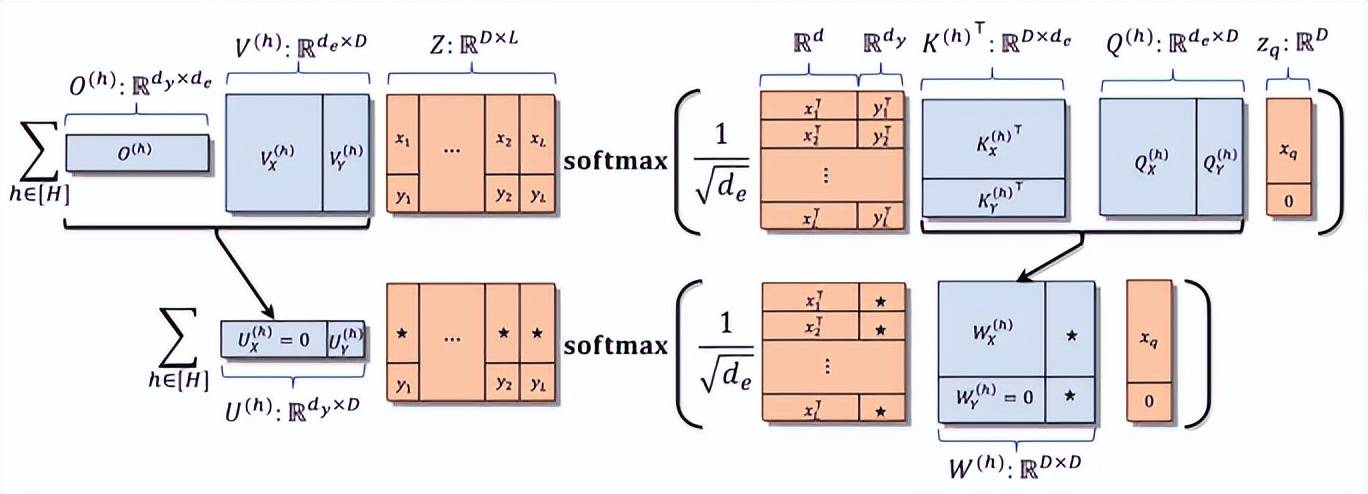（來源：arXiv）
具體來說在本次課題之中，他們研究了訓練多頭自注意力模型（multi-head self-attention model）的優化問題。
尤其是，他們回答了這樣一個問題：在使用一層多頭自注意力模型（one-layer multi-head self-attention model）進行上下文學習時：
首先，梯度優化算法是否能夠收斂？
其次，梯度優化算法收斂到的解統計性質如何？
再次，從網絡結構的角度看，多頭自注意力模型是如何進行上下文學習的？
期間，他們所使用的訓練數據是多任務線性模型（multi-task linear regression）。
特別地，每個線性模型的參數 G 在一個固定的正交基下，有一個分塊對角的分解。
也就是說如果能找到這組基，這個線性模型就可以分解成 H 個獨立的線性模型。
對於每個參數 G，能夠生成 L 個（x，y）對，並且可以讓 Transformer 推測一個隨機的 q 所對應的 y 是什麼。
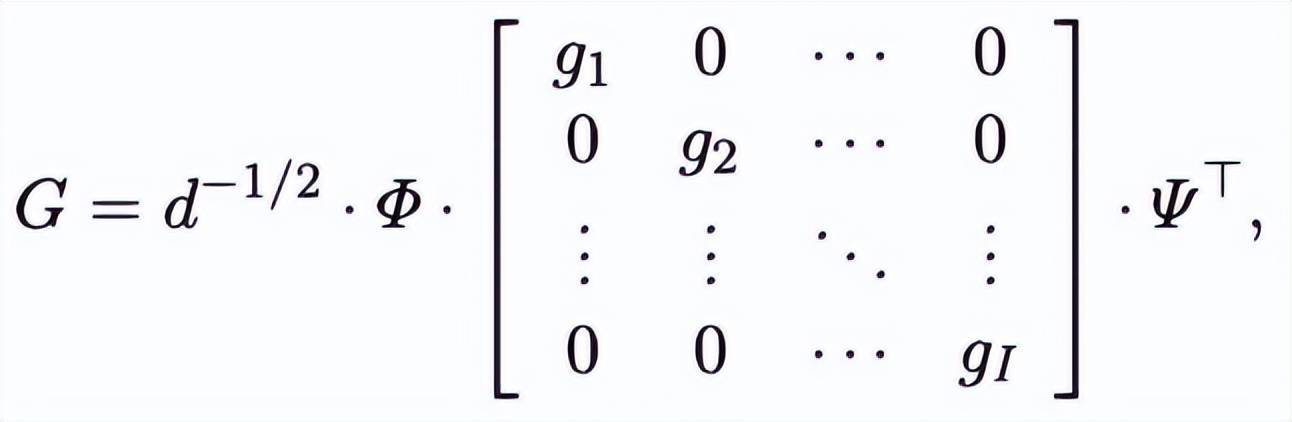（來源：arXiv）
在這種多任務線性數據上，課題組使用梯度流來訓練 Transformer，進而研究這一算法的收斂問題。
通過此，他們發現：梯度流算法的確是收斂的。並且收斂有三個階段——（a）預熱階段、（b）任務分配階段 、以及（c）最終收斂階段。
在（a）這一預熱階段，損失函數緩慢下降。
在（b）這一「任務分配階段」，損失函數迅速下降。並且，softmax 函數使得每一個自注意力頭只關注多任務線性模型的一個任務，該團隊把這一現象稱為「任務分配」。
在（c）最終收斂階段，每個自注意力頭繼續對它被分配的任務求解，最終達到收斂。
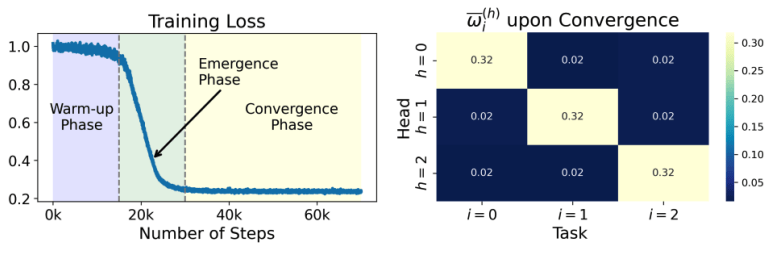（來源：arXiv）
此外，他們還描述了梯度流學習的極限模型的上下文學習預測誤差。
當 （d/L） 趨於零時，誤差衰減到零，其中 d 是線性模型的維數，L 是上下文學習中（x，y）例子的數量。
並且，該團隊還證明多頭自注意力模型，顯著好於單頭自注意力模型。所預測的誤差相差 H 倍之多，其中 H 是注意力頭的個數。
換句話說，注意力頭的個數越多，性能差距越大。
據介紹，該團隊的分析主要基於對自注意力權重的分解。
自注意力機制里主要有兩類權重：QK 權重（query-key）和 OV 權重（output-value）。其中，QK 權重反應著 query 和 key 的關係。
簡單來說，就是給定了 query q（新的輸入）和過去的例子（x，y）的關係。
而 QK 權重反應著 attention 對每一個過去的例子的重視程度。
OV 權重反應著輸出和每一個輸入例子（x，y）的關係，即 attention 如何通過組合上下文學習中的例子從而得到輸出。
需要注意的是在回歸問題裡面，q 是一個輸入，和 x 有一樣的維度，輸出和 y 有一樣的維度。
課題組發現，QK 權重和 OV 權重都是分塊的，並且 QK 權重的 X-X 分塊和 OV 權重的 Y 分塊最為重要。
也就是說，在回歸問題里只需使用 q 和例子裡的 x 比較得到注意力值（attention score）。
在輸出時，只需要根據注意力值（attention score）來合併例子裡的那些 y。
而通過利用數據的線性結構，他們發現 QK 權重和 OV 權重的分塊結構，可以被梯度流算法保持。
更特別的是，因為多任務線性模型的參數 G 可以在某個基下分解，憑藉此他們證明 QK 權重和 OV 權重也是可以被分解的。
這樣一來，就可以把參數的梯度流化，簡為奇異值的梯度流，這時就只需要分析奇異值的變化。
其中，總共有 H*（d_x + d_y）個奇異值，每個頭的 QK 權重有 d_x 個奇異值，OV 權重有 d_y 個奇異值。
而 d_x 是 x 的維度，d_y 是 y 的維度，也就是多任務線性模型的任務數量。
並且，每個自注意力頭的 OV 權重的奇異值，反應著自注意力頭對於對應任務的重視程度。
隨後，該團隊開始分析這些奇異值的變化。他們發現自注意力頭的任務分配基於「OV 權重–每個任務」的原則，來將最大的自注意力頭分給對應的奇異值。
比如，第一個任務被分配給了第一個奇異值最大的自注意力頭。
最終，在梯度流達到收斂之後，根據任務分配機制，每個自注意力頭的 OV 權重只有唯一一個非零的奇異值。
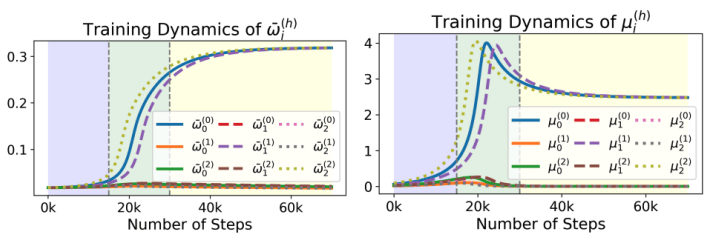（來源：arXiv）
至此，本次研究基本結束。日前，相關論文以《多頭軟 MAX 對情境學習的關註：出現性、收斂性和最佳性》（Training Dynamics of Multi-Head Softmax Attention for In-Context Learning: Emergence, Convergence, and Optimality）為題發在 arXiv[1]。
圖 | 相關論文（來源：arXiv）
陳思宇和王天浩分別是第一作者和第三作者，楊卓然擔任通訊作者。其中，王天浩將於 2025 年秋入職美國加州大學聖地亞哥分校。
圖 | 楊卓然（來源：楊卓然）
不過，課題組仍然覺得自己對於 transformer 和上下文學習的理解還非常粗淺。
目前，他們只研究了一層自注意力模型。後續，他們希望能夠研究多層的自注意力模型。
與此同時，目前他們只研究了線性模型。因此，他們也非常希望研究非線性的上下文學習問題。
此外，目前課題組給到 transformer 的輸入，是獨立同分布的（x，y）輸入輸出數據對，這裡輸入並沒有任何複雜的前後依賴結構。
但是，實際用來訓練 transformer 的數據都是文本數據，裡面有複雜的依賴結構，針對此他們也將繼續加以探索。
參考資料：
1.https://arxiv.org/pdf/2403.00993
排版：羅以