ECCV 2020 | 對損失信息進行建模,實現信號處理高保真還原
編者按:信號在我們的日常生活中隨處可見,例如:聲音、圖像、視頻等。然而在信號的傳輸或存儲過程中,往往會面臨信號失真、質量變差等問題。今天這篇文章就來探討一下信號處理中的信息丟失問題,其中包括微軟亞洲研究院機器學習組與北京大學在 ECCV 2020 上發表的 Oral 論文《可逆圖像縮放》(Invertible Image Rescaling)等工作。
來源 | 微軟研究院AI頭條
大家是否有過這樣的經歷:自己拍攝的高清照片/視頻,想通過社交帳號分享給朋友,然而對方接收到的卻是一張低解析度的模糊照片,甚至有些圖片或表情包在經過多次傳播之後,糊到慘不忍睹。
這種情況是由於程序為了減輕伺服器端的傳輸和存儲壓力,主動對信號進行了採樣、壓縮等操作,而這些操作會不可避免地引起信息丟失(information loss )的問題,造成對原始信號還原的挑戰性。直到今天,信息丟失問題仍沒有被很好地解決。這篇文章將探討信號處理中的信息丟失問題,其中包括的微軟亞洲研究院機器學習組與北京大學在 ECCV 2020 上發表的 Oral 論文《可逆圖像縮放》(Invertible Image Rescaling)工作則以圖像信號為例,探討了圖像的壓縮或縮放後的還原問題。
圖像壓縮算法是將原始圖像壓縮為比特流,圖像縮放算法則是將高清圖像降採樣為低解析度圖像,在實際應用中,二者常結合使用。
圖1:圖像壓縮與縮放任務
此前的通用方法是使用 Encoder-Decoder 框架對降採樣(壓縮 )和升採樣(重建 )進行建模 ,並使用大規模的深度學習模型來取得較好的還原效果。然而,上述框架存在一個嚴重的問題:最後一步從低維信息中還原原始圖像的過程是一個典型的不適定 (ill-posed) 問題。
何為不適定問題?以4個像素點的圖像降採樣為例:
上圖有4個像素,值分別為1,3,5,7。假設對原圖進行雙線性插值降採樣(Bilinear Interpolation ),得到像素值為4的低解析度圖片。那麼,如何從這一個像素還原出原圖呢?這個問題非常難求解,因為有無數多種4個像素取值的組合都可以得到同樣一張低解析度的圖片。如果是 4x 降採樣,則會有16個像素被採樣成一個點。這種不適定問題的產生,就是由於求解過程中的信息不完全所導致的。在降採樣的過程中存在著不可逆的信息丟失, 以至於僅從剩餘的不完全信息中無法很好地還原回原圖。
對於圖像縮放任務中的不適定問題,此前的做法一般是使用一個超解析度的卷積神經網絡,嘗試從大量的數據中強行學習低解析度到高解析度的映射關係;或者使用編碼器(encoder)網絡對原圖進行降採樣,同時使用解碼器(decoder)網絡還原圖片,二者進行聯合訓練(jointly training )來達到更好的效果。但以上這些方法都沒有從本質上解決不適定問題,效果也不盡如人意。
圖2:基於 DNN 的 Encoder-Decoder 結構對圖像進行縮放和還原
不適定問題的產生是由於信息的丟失,那麼具體是什麼信息被丟失了呢?
「High-frequency content will get lost during sample rate conversion.」
——Nyquist-Shannon Sampling Theorem
香濃-奈奎斯特採樣定理解釋說,正是由於高頻信息的丟失導致無法很好的還原高清原圖。那麼如果「保留」這些高頻信息呢?
圖3:經小波變換拆分成低頻與高頻分量的圖片可以被小波逆變換完整恢復成原圖片。
為了可以顯式地保留高頻信息,如果將降採樣的過程替換成了小波變換,由小波變換可以得到原圖的一個低頻分量和三個不同方向的高頻分量。可以看到,這裡的低頻分量與雙線性插值降採樣得到的低解析度結果是一樣的,而高頻分量則是在降採樣過程中被丟失的信息。
當選擇保留全部信息時,可以使用小波變換的逆變換(即反函數,有 , 則其反函數 ),輕鬆地將原圖恢復出來。同理,對於使用 DNN 進行降採樣的圖片,如果保留了全部信息,那麼也可以使用 DNN 的反函數將原圖恢復回來。
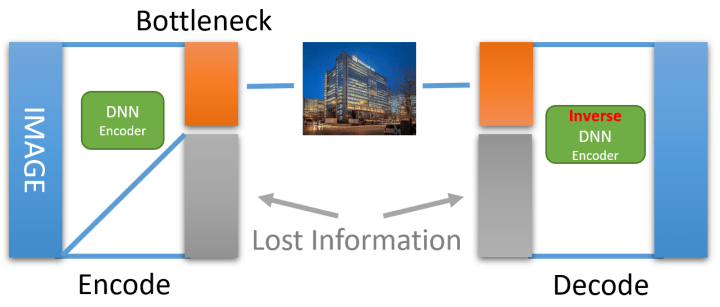
圖4:使用 DNN Encoder 的逆函數、並保留損失的信息即可完美還原原始圖像。
對於深度學習模型這樣一種複雜的非線性函數,它的反函數又是什麼呢?這就要用到可逆神經網絡(Invertible NN, INN )模型。對可逆神經網絡模型不熟悉的讀者朋友,推薦閱讀博客 Flow-based Generative Model:
https://lilianweng.github.io/lil-log/2018/10/13/flow-based-deep-generative-models.html
研究員們採用了最簡單的可逆架構形式(請注意這裡只採用了可逆架構,但建模方式與 Flow-Based 模型不同),且可逆神經網絡是嚴格可逆的。也可以從另一個角度來思考這個問題,即降採樣和升採樣本來就是一對逆任務,那是否應當使用可逆神經網絡。
圖5:使用可逆網絡和其逆網絡來代替 DNN Encoder 與 Decoder
有了可逆神經網絡模型,就可以把之前的 Encoder-Decoder 網絡換成 INN 和它的反函數,這樣,如果可以保留全部信息,那麼就能夠完美恢復出原始的高清圖片。然而,在存儲、傳輸低解析度圖片時系統無法附帶這些本應被丟失的信息(低解析度圖片的維度+丟失信息的維度=原始圖片的維度),而丟棄的這些信息又導致無法使用 INN 來恢復出原圖。到這裡,好像又陷入了一個兩難的局面,那有沒有什麼聰明的做法可以解決這個問題呢?回顧一下前面的簡單例子:
研究員們令 表示原始高清圖片, 和 分別表示低頻與高頻分量。小波變換 將 轉換為 。 本該被丟棄,然而卻無法被丟棄(因為丟棄後無法通過 恢復 ),其原因在於 的分布是依賴於 ,即 是與樣本相關的,因此分布 是難以獲知的。可以發現,只要捕捉到丟失信息(Lost Information )的分布,就能得到關於它最多的信息,所以如果能令 與 相互獨立,並且使數據集中所有的 通過某個變換服從一個預定的簡單分布(如高斯分布),那麼 就可以被安全地丟棄,等需要它時再採樣即可。
到這裡,就輪到 INN 出場了。引入變量 ,令 。 是一個 INN,負責把 轉換為 (這步有定理保證[1])。此時 的分布已經與 無關了,即與樣本無關。同時,INN 還可以生成符合要求的 ,如視覺效果更好的/便於壓縮的低維信息。
圖6:對圖像縮放任務中的損失信息建模
此時,對於與樣本無關的 ,可以放心地將其丟棄。而當需要恢復原圖時,可以在高斯分布中進行採樣來得到 。需要注意的是,整個過程並不是完全沒有信息丟失,這是因為研究員們使用了高斯分布中的一次隨機採樣來代替符合該分布中的一個特定樣本點。但是由於 INN 已經學習到如何將符合高斯分布的點(結合 )恢復為與樣本相關的 ,因此相對於此前完全忽視不適定問題的做法,則可以從本質上緩解求解不適定問題所帶來的困難。該方法在圖像縮放任務上的提升也非常顯著(如下表所示)。
表1:圖像縮放任務在常見數據集上的表現(PSNR)
除了性能的大幅提升,更重要的是,得益於建模方法嘗試直接解決任務的本質問題,模型所需的參數量僅是此前方法的1/10~1/30。下面是效果的可視化,請注意綠色框中對原圖的還原程度。
圖7:效果可視化
對於圖像壓縮任務同理,該方法可以使用對損失信息進行建模的思想應用在圖像壓縮任務中,使用服從高斯分布的隱變量 來捕捉壓縮過程中的信息丟失,從而幫助壓縮圖像的重建效果。對比此前的工作,該方法在壓縮率與恢復效果上都有較大提升。
圖8:圖像壓縮任務中對損失信息進行建模
圖9:對圖像壓縮中損失信息進行建模在常用數據集上的效果
在本篇文章中,研究員們探討了信號處理中常見的信息丟失問題,並採用對丟失信息進行建模的思想,利用可逆神經網絡來最大化還原原始信號,在圖像縮放、壓縮等任務上都取得了較大的提升。了解更多信息,可參考論文以及代碼:
論文地址:https://arxiv.org/abs/2005.05650
相關代碼和預訓練模型:https://github.com/pkuxmq/Invertible-Image-Rescaling
參考:
[1 ]Nonlinear independent component analysis: Existence anduniqueness results
https://www.sciencedirect.com/science/article/abs/pii/S0893608098001403